Ph Formulation
How this might link to other stuff
could be an example of some of the challenges of building a chemical simulation platform
Purpose
There are tradeoffs between FTPx and FCPh, see This internal github issue
However, generally Pressure and Enthalpy is a better formulation of state, because they are continuous variables, and a lot smoother.
The problems all come from temperature. Take for example Water.
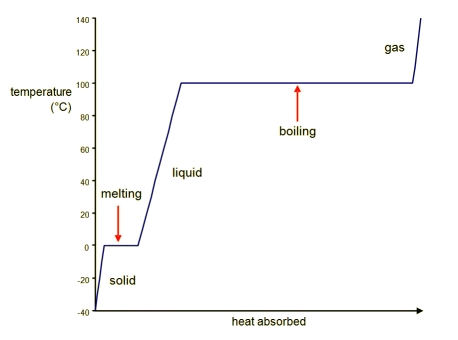
In the melting and boiling points, there are a range of enthalpies that have the same temperature. This is because the water is boiling, and it stays at 100 degrees celcius the whole time. The energy goes into turning the water from liquid to gas, not changing the temperature.
Most solvers work with some sort of gradient descent method (citation needed). Imagine we have the following problem:
Find T= 140
by changing h
(Using the pressure and state constraint equations)
The solver starts with an intial guess of h, , and then changes h based on the nearby gradient wrt temperature.
If the guess of h is within the boiling point, then the gradient wrt temperature is zero, so the solver doesn't know if it should increase or decrease h. This means it cannot solve the problem.
While this problem can be reformulated to solve for t directly, this is not generalisable in the case of an unknown model, and would require different reformulations for different property packages that are supported by the platform.
Research Questions
What is a more generalisible way of reliably calculating state properties of compounds, given discontinuities such as in temperature, regardless of property package structure?
Method
One way to solve this problem is to change the formulation so there is no zero gradient. In a higher pressure, the boiling point is higher, so rather than fixing pressure directly (P = 101325) we set it based on the enthalpy (P = 101325 + 0.0001 * h)
increasing the pressure as the enthalpy increases adds a slight "skew" to the graph, meaning that when h is higher, the boiling point is higher, therefore the temperature is slightly higher too.
This does add some amount of error to the result, as we are no longer setting the correct pressure. However, it provides a pretty accurate guess of the correct h for the given temperature.
The error can be reduced by updating the pressure constraint so that the "skew" is centered around guess for h. This means that at that enthalpy, the pressure will not be adjusted at all (and in nearby regions, the adjustment will be very small:)
P = 101325 + 0.001 * (h - calculated_h)
This formulation will yeild a better guess for h, and can be repeated iteratively for better results.
Theroetically, the whole problem can be considered an optimisation problem, and solved by a mathematical solver, trying to find the value of h where it doesn't matter if the skew is 0.001 or 0.1, the temperature and pressure is still the same. So far I haven't got that working.
Another way we can formulate it is that rather than changing the pressure constraint, we can fix the pressure directly and change the temperature constraint: from
T = 140
to
T = 140 - 0.001 * h
In this constraint, changing h also means you get slightly closer to the target temperature, and so this also fixes the problem. It has the added benifit of not requiring an additional constraint for pressure, thus making the problem simpler (you're only optimising for temperature now if you know the pressure.)
The same principle can still be applied to "recenter" the guesses for h around what the target temperature is, to avoid extra skew in subsequent iterations
T = 140 - 0.001 * (h - calculated_h)
Findings
Discussion
See also: Ftpx Vs Fphx
Backlinks